A simple note on Bitcoin and Blockchain Technologies.
Date : 15/06/2018
Version: 1.5
Status: Ready. It will remain a working document anyway.
By: Albert van der Sel
Remarks: It's a very simple note on Bitcoin Technologies. Hopefully..., I will not bore you to "death".
Original location, and where this doc will be maintained: www.albertvandersel.nl
Please refresh the page to see any updates.
Note on Februari, 2019:
Blockchain is just a useful technology. There is nothing wrong with it.
It's just a technology, and you can use it for countless applications.
But specifically with cryptocurrencies: I stopped to like them. I think it's a bad idea,
at least in the form they can be accessed today. The latter is an important point for me.
What is it what I think is wrong? Suppose a person has a considerable sum in bitcoins.
Then that info is stored in the "Bitcoin blockchain". Now, people with bitcoins, may store
their private keys in hidden places, only known by them. Suppose that person dies, or gets
an accident, and is not able any more to communicate. In such cases, the money is gone.
The money is gone, and even close relatives are not able to get it, even if they are
morally fully entitled to it.
The system is designed to eliminate central institutions like Banks. It's indeed a form of
direct money transfer.
There still is no adequate and secure manner to recover truly lost keys, or access funds
without keys, while you are (morally) entitled to it.
Ofcourse, digitally storing keys at mutiple places, or have keys on paper, or barcode,
or whatever appropriate way, can help overcome lost keys.
But people are just people, and some have fallen into the "trap", and the assets are gone.
There should have been implemented a nifty "zero knowledge proof of ownership", since
technically, and viewed from an organizational angle, it could have been realised.
In short: I don't like the coffin-like "traps" inherently present with those systems.
It took a while, before I gradually got this angle to look at it.
I think that almost everybody will disagree with such angle to look at it.
And indeed, I don't belong in the "investors world" and "speculative investments".
This note is not about "making money...". If, in that respect, you would listen to me,
you would be broke in recordtime.
Instead, It will cover (in a lightweight fashion), some important Blockchain related technologies,
using the Bitcoin system as the "vehicle" to present the information.
It's not so much the "currency" that I am interested in, but the array of Technologies
makes a study worthwile. By the way, from all cryptocurrencies, the Bitcoin seems pretty
promising, and certainly "secure".
Anyway, in this note, "The Bitcoin system" is the vehicle to show some of those technologies.
Lot's of interesting concepts were brought alive since (around) 2009. Some new concepts, and some others
which were devised decades ago, but found an implementation in bitcoin technology, and other cryptocurrencies.
Along the way, I discovered, that it is a pretty tough study. But I hope to say something useful on the subject,
and not bore you to "death". The latter statement is a serious risk, and I am fully aware of it.
IMPORTANT:
- If you are only interrested in Theory, then there is no warning in effect.
- However, if you actually own bitcoin(s), or are planning to do so, then make sure
that you fully understand how to backup your wallet, and keys. There are multiple "sorts"
of wallets, but they all contains your keys, and those keys are critical for "ownership" of coins.
Study the types of wallets, like "a paper wallet", or "deterministic wallet", where keys
have a common "seed", which might help to prevent nasty situations.
Also, take a good look at the pro's and contra's of a "hardware wallet".
Study how to backup-, and saveguard your keys, and how to recover if some sort of error occurs.
Also, be carefull not to restore an older wallet backup after you have performed transacions.
As another safety aspect: it is advised to govern your wallet(s) yourself, and keep it save from others.
Also, strong password protection on wallets and/or keys is advised.
Sorry for those very trivial statements.
Main Contents:
1. Quick Overview.
1.1 Quick overview: Blocks and the Blockchain.
1.2 Quick overview: The fields in a block.
1.3 Quick overview: The "Wallet".
1.4 Quick overview: The Bitcoin Network.
1.5 Quick overview: The Bitcoin Address.
1.6 Quick overview: Hard- and Soft forks.
2. A few words on security/crypto methods, used in Bitcoin Technology.
2.1 A few words on Symmetric and Asymmetric encryption.
2.2 A few words on Hashfunctions, Hashes and Digests.
2.3 A few words on Elliptic key encryption (Asymmetric encryption).
2.4 A few words on Bitcoin Theft.
3. The process of Mining, and Transactions.
3.1 A few words on Mining.
3.2 More on Addresses.
3.3 More on Transactions.
4. Just a few words on Smart Contracts.
1. Quick Overview.
1.1 Quick overview Block and the Blockchain.
Fig 1: Just an illustration of a few Blocks in the blockchain.
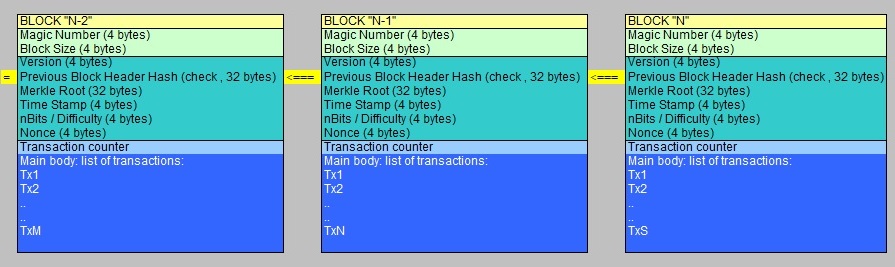
Source: my own Jip and Janneke figure.
The blockchain is indeed a chain of blocks. That sounds absurdly simple. It is. It is a linked list
of blocks, which together register all transaction which have occurred sinds "Genesis", which was the
time (more or less) when the first block was devised.
Today, a block is about 1 MB of size. It has a Header (the dark green part, starting with the "Version field),
and a "body", listing all transactions in that block (the blue part).
Note from figure 1, that each block, has in it's header the socalled "Previous Block Header Hash".
This functions as a sort of Block ID, but it is calculated from the header of exactly the Previous block.
So, if we take a look at block "N", it's "Previous Block Header Hash", was calculated from
the "Previous Block Header" of Block "N-1".
This guarantees unique 32 bit strings in each block.
The whole blockchain is copied (or in better words: is distributed) among many computer systems.
Today, this number of computer systems already is very large.
If you would like to cheat, for example by modifying a block, it would not agree with the many
distributed copies of the chain, on all those other computer system.
The faulty change would not be committed in the system, and simply will be rejected.
Most security experts would indeed say that this protocol, is practically impossible "to hack".
Another very interresting element, is the fact that blocks which are already fully added in the chain,
are considered to be "immutable|. So, they cannot be changed.
Indeed, this results in a very trustworthy form of bookkeeping.
The full list of "links" of those "Previous Block Header Hash" in all those blocks, garantees
a sort of "general ledger" which practically cannot be tampered with.
Note that a "Block" is not litterally a sort of "container" for bitcoins. It's purpose is to securely
register "transactions" with bitcoins (or other cryptocurrency which uses another form of Blockchain).
In figure 1, transactions are simply denoted by "Tx", but those sort of records have a deeper structure ofcourse.
By the way, the notation of "Tx" is in used Database Theory in general, to denote a "transaction".
But, your "funds" in bitcoin, is indeed stored in the Blockchain. How is that possible?
Just like with normal/regular banking, all payments and what you received, is registered (or stored),
completely in the full blockchain. So, your netto saldo can be deduced from the blockchain.
So where is your money? As records, possibly dispersed over various blocks, in the Blockchain.
Note that this is not much different from traditional payments. If "Company A", pays 100 euro's to "Company B",
then the account of "Company A" is lowered with 100 euro, while at the account of "Company B", 100 euro's is added.
No one is running around with 100 physical euro's. It's just a digital transaction.
The whole lot of transactions, over time, determins your current saldo/
Note that the "blockchain" is a "replicated" database, where a copy resides on each "node" (computer),
which participates in this "peer-to-peer" network.
You can download the "bitcoin client software", and have such a copy of this "replicated" database
on your own system. The software will always try to "sync" with the other nodes.
Note too that this distributed system, completely lacks a "central authority", like a Bank or
other main financial instute.
Until recently, it was indeed organized in such a way, that every "full node" (see 1.4), stores
a copy of the blockchain, holding all committed transactions. This is still true. What is also still true,
(but likely to change a little, soon) is that a transaction must be committed to the blockchain first,
before it can be stamped "as done". As the number of users increase, this slows down the performance.
It has been argued, that the Bitcoin system has an intrinsic "scaling problem", in terms of the number of
concurrent transactions.
Late 2017, and in the first few months of 2018, the new "Lightning" protocol was tested, and
indeed begun implementation. Transactions now, might be committed "off-chain" first, and only the "endresult"
is written to the Blockchain. See section 1.4.
A protocol change (or other fundamental change) for the Blockchain (or Bitcoin system) is often
formulated in the format of a "Bitcoin Improvement Proposal" (BIP), which has some resemblence to the
RFC's for Internet protocols.
1.2 Quick overview: the fields in a block.
At this stage, there is no need to inspect all fields of a Block. However, some are really
easy to understand. Others are a bit more involved, and are discussed at a later moment.
Most bitcoin experts say that the "raw header", is that piece of the block, 80 bytes long, which shows in
in figure 1 as the darker green part ("Version" up to the field "Nonce").
The very first two fields, are the "Magic Number" and "Block size". A magic number is generally
a field which identifies a type of block (or file, or other structure). So, all blocks use the same
constant value, of 0xD9B4BEF9, which simply says, that this is a "bitcoin blockchain" type of block.
So, nothing special here.
The "Block size" indeed specifies the size of the Block. This field is 4 bytes long, meaning that
in principle 232 numbers would be possible. For now, it is simply the number of bytes from start
to the end of block. The original "designers" of the Bitcoin network/protocols, just took 1MB
as the maximum Block size. That number is debated among bitcoin users and designers.
There are always pro's and contra's for a smaller or larger blocksize. Regularly, proposals are launched,
to change to maximum blocksize.
Above, we already have touched upon the "Previous Block Header Hash" field.
New blocks are added to the end of the chain, at a (sort of) average rate of one every 10 minutes.
Every new block must "fit in" into the chain. From the former block, a hash (security object) is calculated,
and that hash will be stored in the "Previous Block Header Hash" field of the current block.
This way, we get a "well-knotted", linked list of blocks.
The Block "height" is often said to be the block number, which is the count from the very first block,
up to the block under consideration (e.g. block number 101233).
However, occasionally, different miners (later more on this), may produce a new block at the same time (more or less),
and temporarily two blocks exist with the same "height". This will be resolved somewhate later, by the system.
For this reason, and others, the best identification is the block's "Previous Block Header Hash" field.
However, the Block "height", or Block number, remains heavily used to identify a certain Block.
The "body" of a block, is formed by a transaction listing.
The full blockchain, registers all transactions that ever occurred, and transactions that will occur.
We must still investigate the process of "Mining", but miners constantly trying to create new blocks,
which will hold recent transactions.
A transaction holds security information (public key and signature) of the entity (or person)
who initiated the transaction, as well as a bitcoin address which represents the destination for a bitcoin payment.
1.3 Quick overview: The "Wallet".
There are several forms of "wallets". You can for example have "bitcoint client" software
on your computer, which includes a wallet. This wallet contains a (strictly personal) "private key", and a "public key".
The keys are stored in the wallet file.
The "mechanics" of the keys and elliptic cryptography, will be touched upon in chapter 2.
For the wallet, you generate a private key of 32 bytes, which is 256 bits. Then, using something called
"elliptic cryptography", the software generates a public key. This key may indeed be "public", since it's
quite impossible to derive the private key from this public entity.
Your public key, is also sometimes called your "wallet address". It's also equivalent to your bitcoin address,
and later, more on that remarkable fact.
Indeed, your public key is a tool to identify your bitcoins.
So, the blockchain has registered your public key in one or more transaction.
For performing a transaction, your private key is needed. Your local software creates a security identifier,
using your private key, which identifier can be "matched" to your public key. It is important to understand
that your private key is never send, or "as is", is used in transactions. It's a derived identifier
which proves that you are the owner of a bitcoin address.
When you indeed own bitcoins (or fractions thereof) you must be extremely carefull
with your private key(s), and keep them save.
All transactions are broadcast between nodes, and begin to be confirmed/committed by the network,
usually within the next 10 minutes (or so). At least, this is how it was, not too long ago.
The Lightning network will generally change this.
A process called "Mining" is, and remains, critical for collecting transactions in a new block.
Your wallet(s) contains your keys, which are critical to prove your ownership of Bitcoins.
Therefore, you should also make sure to know how to backup your wallet/keys.
Secondly, keys stored on portable devices should only be used for small transactions.
In the Appendix, you will find some of my recommendations, but the Internet is full of good
articles providing good advice how to saveguard your keys.
The exact mechanics of transactions are fairly complex, and I think I will try to say something usdeful
in Chapter 3.
1.4 Quick overview: the Bitcoin network.
Originally, the Bitcoin network, is a Peer-To-Peer network, just using the Internet.
Peer's (which are computers running Bitcoin software), know other peers, and they know
other peers etc..
The nodes on the network may have higher number of reponsibilities, or a lower number of responsibilities.
Generally, we have:
-Full nodes, storing the full blockchain (in May 2018, it was about 160 GB), with a higher number of tasks.
-Lightweight nodes, or Partial modes, not storing the full blockchain. They have a much less number of tasks.
-Mining nodes, which are one of the above, but also using algolrithms for "solving the puzzle".
-Archiving nodes, which may upload to new nodes, and a number of other tasks.
Full nodes will sync and must have the full chain. Ofcourse, except for the blocks which are about
to be computed soon. Then, afterwards, those blocks also must sync to full nodes.
Full nodes have also reponsibilities as data format checking, semantics, valid identifiers. Full nodes will participate also
in consensus checking. The latter term is very interresting and must be explained a bit later.
It's at this point not possible to explain it correctly and more in depth, without first studying "Mining"
and what the relations of Mining are, with Full- and Partial nodes.
For example, Full nodes will transmit new transactions from users to miners, where the latter will compute
(eventually) new blocks. They "mine" blocks with new transactions. This is a difficult task.
There is no problem at this point, since this section is simply a quick overview.
Nodes in the network may exchance blocks, but the RPC protocol is also heavily used. In this case,
this is JSON-RPC, meaning that short "messages" are send to a remote Host, in order to active
procedures overthere, doing certain work. RPC is a well-known protocol, used in almost any type
of network. Many programming environments have API's for calling RPC's.
In general, the Bitcoin community advises to run Full nodes, also in order to add to consensus checking,
which was not explained at this point. However, it's a protocol which ensures that the Bitcoin network
and it's objects (blockchain) stays "integer".
Lightning:
The question is, if exchange of blocks add to a performance bottleneck. Intuitively, the more blocks
will come into existence, and computernodes will get alive, and users connect, the more delays are to be expected.
However, the above is only partially true, how strange that may look at first sight.
if users choose to run full nodes, then this will help alleviate performance issues.
Presently, the Bitcoin "process" (generating new blocks, committing in blockchain) can handle a very limited number
of transaction per second. Somewhat later after 2009, concerns about the scalability of the Bitcoin network
became an issue.
The number of committed transactions will vary per day ofcourse, but various graphs on the internet
shows a typical number of around 200000-300000 (or so). Don't take this as a fixed number.
It's just for illustrational purposes. So, if there were indeed 300000 transactions at a certain day,
then we would have on average 300000 Tx/86400 seconds = 3.47 Tx/sec.
Ofcourse, on peak days it would be somewhat higer.
But indeed, the architecture of collecting Tx in new blocks, mining, and finally storing in the blockchain,
limits the number of transactions / second.
A good remedy (might) be the "Lightning network"
It's oriented mainly around "off-chain" transactions and commits, and sharing and chaining of channels.
Say that Alice and Bob want to perform a transaction. The core "trick" is formed by the fact
that they "open" a channel and a temporary construct, what has some resemblence to a wallet.
This construct then will register transactions. Even if Alice, Bob, and possibly other parties
have concluded their sub transactions, then only the "end resdult" will be written back
on the Blockchain. Note, that thus almost all interactions of those users is "off-chain",
which constitutes an enormous performance improvement.
The Lightning network, will benefit from the "SegWit" soft fork (see chapter 3), which represented a different way
to store transaction data. Data still remains in the block, but scripts and signatures
are moved to a new part of transactions. It turns out that more transaction can be stored per block,
which helped in upgrading the transaction rate.
1.5 Quick overview: the Bitcoin address.
When you start using Bitcoins, a Bitcoin address is needed.
It represents an identifier where funds can be transferred to.
There are several "methods" by which an address can be generated:
P2PKH (or "Pay to Public Key Hash"), P2SH (or "Pay to Script Hash"), and Bech32 (a SegWit address format).
The first one works like this: The appropriate bitcoin client software, generate the Private key first.
From this Private key, the corresponding Public key is generated. Lastly, by (a.o) hashing that Public key (multiple steps),
you get your Bitcoin address.
For information about keys and hashing: see chapter 2.
In the Bitcoin system:
- a private key is 32 bytes long (or 256 bits).
- a public key is 64 bytes long, or 65 bytes, or 32 bytes (depending on coordinate perspective) (*).
- a public Bitcoin address is derived, using multiple steps from the Public key (P2PKH), or by another method.
There exists thus various formats of Bitcoin addresses.
(*): there is a small issue in directly specifying the length of a public key, since in
elliptic cryptography, it is technically a coordinate like (x,y). Later more on this.
Basically, using the common P2PKH, a one way direction is formed by:
Private Key → Public Key → Bitcoin address.
The derivation of the adress involves steps using SHA-256, RIPEMD-160 and Base58Check.
The above is not the only route to obtain a Bitcoin address.
We have no choiche than to pospone a proper discussion after some chapters with more info.
This is indeed a rude and very high-level representation.
For more details, we need to check the chapters below.
1.6 Quick overview: Hard- and Soft forks.
There exists multiple (>2) meanings of the term "fork" (in the context of Bitcoin), but the
most important ones are Hard forks and Soft forks.
The blockchain may temporarily diverge in two "chains" (or apart streams of blocks), or even
permanently diverge in two chains.
It's possible that sufficient people or groups, want a fundamental change in one of Bitcoin's protocols.
As usual, most of the time, there will be supporters for such change, and people who are opposed
to that change. A change is often formulated in the format of a "Bitcoin Improvement Proposal" (BIP),
which can be evaluated by the users of the network. This looks a lot like the "RFC" mechanism in Internet.
A change which is often discussed is the Block size. And indeed the "Bitcoin Cash" system, hard-forked off
from Bitcoin, at august 2017, now using a Blocksize up to 8MB.
This was indeed a hard fork. It's often defined as a permanent split from the legacy Block chain.
The hard-fork does not have backward compatibility, and blocks from one system will not be accepted
by the other system.
A soft fork is a protocol change too, but still backward compatible with the former format.
For example, the "SegWit" change was a "soft fork". It did not disrupt the Blockchain, and did not gave
rise to divergence.
In short: Hard forks means a chain split, a soft fork is compatible with the former chain, and no split occurs.
A hard fork occurs when a change is implemented in a software upgrade. The un-upgraded nodes, may not
validate the new blocks, while the upgraded nodes, do. It may result in a split of the chain,
followed slightly later by two different software paths.
New functionality, or a change in a protocol, from a usergroup (written in a BIP first), may initiate
the intention for a hard- or soft fork at a later time. Miners also may have a large influence
in the process, since if an increase in fees are involved, they are motivated to support the change.
A fork should always be announced, and a start day, or flag, should be determined.
It's also possible that a proposed change, which would result in a fork, is generally rejected.
It means that the degree of consensus throughout the entire network is decisive for the implementation
of a fundamental change.
Interestingly, there exist multiple interpretations of hard- and softforks. It simply means that
articles other than this simple note, may deviate from the info above. However, most articles
are in line (sort of) with the info in this section.
This concludes Chapter 1, a "Quick Orientation".
It's also really usefull to read the original article of Satoshi Nakamoto, the "Inventor" of the Bitcoin system.
Here you will get an appreciation of the original intentions and motivations.
You can find that document here
Note that Satoshi Nakamoto is likely to be a pseudonym, for either a real person,
wishing to stay anonymous, or a group of unknown persons, who invented the Bitcoin system.
2. A few words on security/crypto methods, used in Bitcoin Technology.
A crypto expert, could easily write a 800+ page text on this vast collection of subjects.
And..., then that would cover only the basic theory.
Don't forget that new articles popup daily, covering new territory.
Also, a large part of Quantum Computing deals on crypto- and related theories.
I guess that I only want to say that the subject is "huge".
Here, just a few points will be touched upon, which are, I think, relevant in a Bitcoin discussion.
It's probably much better to take a look at Wikipedia docs on this subject, because my story here
is extremely simple.
2.1 A few words on Symmetric and Asymmetric encryption.
Bob and Alice are two well-known persons, which are often used to illustrate cryptographic events. But they often show up
in other sciences too, like in Quantum Mechanics to illustrate Quantum effects and observations.
=> 1. Symmetric encryption - Or - Shared key/Secret key:
If Bob and Alice want to exchange encrypted messages (meaning any type of data, like files, mail, http etc..),
then they may use one single shared key, to encrypt and decrypt those messages.
It's important to understand that both use the same key. This key must stay secret from other people and entities ofcourse.
This is often seen as a weaker point in the protocol: that is: how to safely get the key to both parties?
Maybe they need some sort of "secure" channel first, to transfer the key, for example from Alice to Bob.
All encryptions/decriptions go by using the same one key.
=> 2. Asymmetric encryption - Or - Public key and Private key:
In this case, a user has a Public key and a Private key. It's a "key pair". So, that holds for Alice and Bob too.
The "private key" must be kept strictly private to the owner. The public key may be known to other user(s).
Such a Public key, and Private key (for a certain user) are related in such way, that an encryption with one key,
can be decrypted with the other.
So, if we take a look at Alice: she safeguards her private key, and never discloses that to another person.
However, she may send her public key to Bob. Likewise, Bob may send his public key to Alice.
Now, the "keypoint" here is:
-That Alice may use Bob's public key to encrypt messages. Bob can decrypt them, using his private key.
-Bob may use Alice's public key to encrypt messages. Alice can decrypt them, using her's private key.
-Any other user who intercepts such message, cannot do anyting with the encrypted data.
The Jip and Janneke figure below illustrates the difference between Public key/Private key, and Shared key encryptions.
Fig 2: Just an illustration of Public key/Private key, and Shared key encryptions.
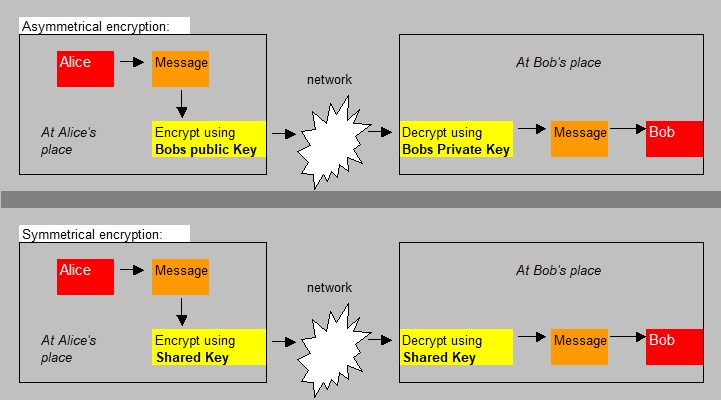
Source: my own Jip and Janneke figure.
=> 3. Asymmetric encryption, with symmetric encryption (shared key):
Public key/Private key cryptography is generally considered to be "better" than Shared key cryptography.
However, the first method is more involved and has a higher overhead.
For large data transfers, Shared key performs much better. However, how both the sender and receiver
gets the same one shared key, was always a point of concern. Obviosly, if the intended sender just
sends the (readable) Shared key to the intended receiver, then "someone" on the network
may intercept that key, and then this "someone", has the option to spy on the messages.
Therefore a "2 Stage" approach is often used.
Using Public key/Private key cryptography, the "shared key" is simply a message, which is
thus enveloped by the first type of cryptography. Once both parties posess the same shared key,
then the encryption of data fully switches to the symmetric type of encryption.
There are quite a few variants (sorts) of both "Shared key" and "Public/Private key" implementations.
Although the general methods described above is true, the variants differ in bitsize, contruction of key(s) etc..
Examples of Symmetric Key implementations (thus: shared key):
AES-128, AES-192, AES-256, RC4, RC5, RC6, DES.
Examples of Asymmetric Key implementations (thus: public key/private key):
RSA (like RSA-256), DSA, Elliptic curve techniques.
The Bitcoin system uses "Elliptic Curve Digital Signature Algorithm" or ECDSA, based on
Elliptic curve cryptography.
What we have seen above, is typically used to encrypt/decrypt data. Something that is called
a "hash", or "digest", is an other sort of implementation.
2.2 A few words on Hashfunctions, Hashes and Digests.
For a general understanding of the idea behind a "function", it is generally understood that it can take an input,
and maps to a certain output.
In math, this is ofcourse an extremely well-known concept, like for example f(x)=2x+7, or f(x)=3x2 etc..
So, for example with "f(x)=3x2", we can say that for any "x" (in it's domain), we can
find the corresponding (output) value "3x2". Thus, suppose x=3, we have the output f(x)=3*32=3*9=27.
A special class of functions in cryptography exists too. These are the hashfunctions.
They can take data of variable length, and produce output of a fixed size.
This output is often called "the hash", or "the hash value", or "the digest".
Almost always, different inputs will generate different outputs. Usually, if in an exceptional case,
two different inputs result in the same output, it's called a "collision".
However, it should be understood that "in crypto appliances" these should be extremely low or non-existent.
-If you let operate the hashfunction on some input, it produces certain output.
If you again let operate the hashfunction on that same input again, then it must produce the same output again.
In crypto language, it is often said "that if we apply the hasfunction on a fixed message,
then it always results in the same hash (or digest)."
-Generally, it is understood that a hashfunction is "one way". It's easy to get an output,
but say you have a given output, it should be practically impossible to find the associated input.
Suppose we have a simple example of a "password hash", created by the password hash function Η.
Then for example, Harry could use the readable password "MyStrongPWD", which might be mapped as:
Η(MyStrongPWD) → 045A77BBC190FFBB7CC7745
Also, suppose Mirja uses the readable password "IwantSummer", which might be mapped as:
Η(IwantSummer) → 095A76EBC140FCBA7CA3212
Note that the length of the hashes are equal.
There exists quite a few cryptographic hash functions. A few, which once were considered
to be "strong", were MD5 and SHA-0. However, around the period 2003-2009, some weaknesses
were found, and MD5 is currently not advised anymore.
Some weaknesses were found in SHA-1 too. Currently the SHA-2 and SHA-3 families, are still
considered to be very strong.
It should be understood, that if a genuine "brute force" is applied, many so-called
secure stuff, can be broken. That is, if enormous loads of CPU power is applied,
and for example runs for a year (*on average*), before a hash is cracked, you might still
consider it to be rather secure.
Indeed, it should be extremely difficult to derive the original text from a hash.
Note: some hashfunctions use variable properties in order to establish the hash,
like the system date/time, or cpu params etc..
These would not be "deterministic" (e.g. the same input must give the same output over and over),
so, in general, these are not suited for many functions in cryptography,
but ofcourse they can be useful in other applications.
Digital Signature:
You should see this feature, as a (sort of) special case of asymmetric encription.
A Digital Signature, at creation time at the sender, uses the Private key from Asymmetric encryption,
and with verification at the recipient, the Public key of the sender is used.
The main purpose is to provide trust to a recipient, that a message is indeed from an intended sending party.
If the intended sending party, indeed already have a Private key, and a Public key to it's disposal,
then a signing algolrithm uses the properties of the message, and application of the Private Key,
"to sign" the message. The recipient then, uses the Public key of the sender to verify the signature.
One main relevant application of this in the Blockchain, is that every transaction of an owner,
carries the Digital Signature of that owner (generated by his/her Private key), which can be verified
by using the corresponding Public key of that owner.
2.3 A few words on Elliptic key encryption (Asymmetric encryption).
Let's see what this remarkable stuff is about.
2.3.1 Elliptic curves.
The Bitcoin system uses "Elliptic Curve Digital Signature Algorithm" or ECDSA, based on
Elliptic curve cryptography.
This is used for the derivation of the Public key, given a Private key, and thus also
effects the Digital Signature used in the Bitcoin system. If needed, see sections 2.1 and 2.2 above.
An "elleptic curve" has a general equation y2=x3 + ax + b
Note: In math, it is shown that the real general equation has more terms than is shown above.
You know that functions (or relations) of one variable, that is, in the form of "y=f(x)" are often plot
in a two dimensional plane, having an x-axis and y-axis.
So, for example, a sketch of y=2x2 can easily be drawn, if you take the x values from say
ranging from -5 to +5, thus if x takes on the values -5,-4,-3,-2,-1,0,1,2,3,4,5, and for each of them,
calculate the corresponding y value. You then will see that y=2x2 is a parabola.
Ofcourse, here I took "x" to have integer values, but generally, this math is based on "real" numbers.
You could plot an elliptic curve too.
The Bitcoin system uses ECDSA, based on the elliptic curve y2=x3 + 7
You might wonder why this specific equation is used, and also you might wonder how a Public key
is generated using such curve. I will try to explain that in a moment.
In ECDSA, once a Private Key is established, we go to work using the elliptic curve.
That is, we use the elliptic curve, to derive the Public key.
Fig 3: Just an illustration of a particular elliptic curve.
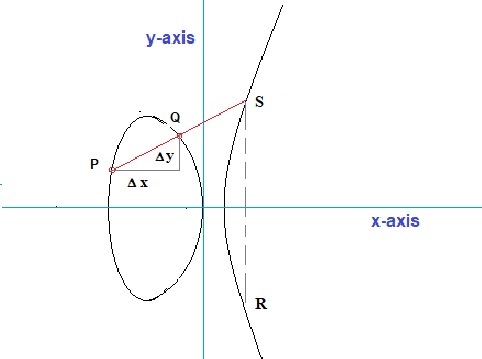
Source: my own Jip and Janneke figure.
Depending on the coefficients "a" and "b" in the relation above, the form of such curve
can vary greatly: just google on pictures of "elliptic curve", and you will see that variety.
Such a curve defines an abelian group, if the members in the group (thus the points on the curve),
adhere to a few basic rules. One of the most important rules is "closure", meaning that
an "operation" must exist, say denoted by "+", in such way, that for all members "P" and "Q",
must hold that P+Q is also member of the group (thus also a point on the curve).
It's tempting to view "+" as the addition operator, as is used in arithmetic.
Almost, but not exactly the same thing. However, in all crypto literature, or math articles
dealing on elliptic curves, the operator is indeed called "addition".
However, it is addition of any two points P and Q. For example, vector addition also
looks a tiny bit different from simple regular addition, as is used in arithmetic.
Thus the only requirement is that "adding" points, no matter how many times, must produce
again a point "somewhere" on the curve.
How would one geometrically, or algebraically, further define the exact mechanics of such an "addition"
for any members on an elliptic curve?
- Viewed from a geometrical perspective, you only have one logical option: draw a straight line through P and Q,
and see where it intersects the elliptic curve. That point then would be the "result" (apart from
from a negative sign). You cannot opt for another solution. For example, any sort of curve between P and Q would not work,
since you want one result for P+Q, and not an unknown (variable) number of other solutions.
A line is logical, but also remember that we are constructing an "addition operator", in such way,
that P+Q actually works. That is: producing a third point on the curve (member of the curve).
Viewed this way, we can say that a line through P and Q, exactly fits our "construct".
There is only one small catch. Using the principle above, we find the point "S" (see figure 3),
but ultimately we need to arrive at point "R". Here then, is a small difficulty to explain why
we must "flip" the "y-coordinate" of point S, to get the coordinates of R.
- Viewed from an algebraical perspective, you can say this:
See figure 3. You see just some randomly chosen points P and Q. I could have taken any other set,
with one exception only: when P and Q have the same "x" value, since then a line between P and Q
would go to "infinity", and never intersects the curve.
Suppose we need to express "P + Q = R" in coordinates (x,y). Here then, the aim is to find
the coordinates (x3,y3), if P and Q are expressed as (x1,y1) and (x2,y2).
But, we will introduce an intermediate step, namely finding the first true intersection "S" first, and
if that succeeds, we will immediately find the point "R", since the points R and S only differ in the sign
of the "y coordinate". Why we need to flip the y coordinate, will be explained later.
Please refer to figure 3 again. We are going to solve "P + Q = S" in terms of coordinates.
We then would have: (x1,y1) + (x2,y2) = (x3,y3)
Note that the "slope" of the line through P and Q, or in better words, the "gradient" of the line through P and Q is:
grad = (y2 - y1) / (x2 - x1) = Δ y / Δ x
Let's call this gradient "λ".
The general equation for the line between P and Q is:
y=y1 + λ (x-x1)
We need to find the intersection of that line, with the elliptic curve. So, having two unknown variables (the coordinates),
and two equations, provides us mathematically with everything needed to find the intersection S,
and thus we can find the coordinates of R too.
Both equations together, that is:
| y=y1 + λ (x-x1)
| y2=x3 + ax + b
will provide the solution for the untersection point "S". Believe me, it's just a bit of math, and nothing more.
Above is just an outline. Before we can make this more concrete, we need to return to the purpose of this excercise.
So, what is the purpose anyway? Knowing that adding points which are on an elliptic curve, must result in another point
on that curve, might be nice, but so what?
Instead of adding different points, like P and Q, we can also do "an experiment" like Q+Q.
If you look at figure 3 again, you can visualize what it means. Take a look at figure 3 again.
Now, let point P, along the curve, "crawl" towards point Q. At a certain moment, they coincide.
The line through P and Q (actually through Q and Q), is now exactly the tangent line along the curve,
at the point Q.
The tangent line will intersect the curve somewhere at "T". This new point "T", is the result of "Q+Q",
except for the fact that we still need to flip the y-coordinate of T, to get the real result of "Q+Q",
but I ignore that for a moment.
You can repeat such addition over and over. You can actually try for example:
5 * Q = Q+Q+Q+Q+Q
or:
n * Q = Q+Q+...+Q (n times)
2.3.2. The Bitcoin Elliptic encryption "secp256k1" ECDSA Protocol.
-Here, the "secp256k1" SEC (Standards for Efficient Cryptography) specification is used.
This specification lists all relevant parameters for a specific elliptic curve and encryption.
-It uses the elliptic curve "y2=x3 + 7", which you can find
from the general equation "y2=x3 + ax + b" and with "a=0" and "b=7".
Fig 3: Just an illustration of the secp256k1 elliptic curve y2=x3 + 7.
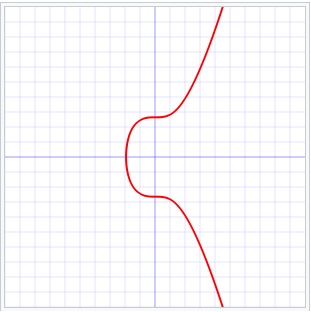
Source: Wikimedia commons (Public Domain).
-However, the x domain (the x-axis) is not the familiar set of (continues) real numbers, but a discrete set
of numbers for which the specification is set in "secp256k1".
Using this set of "x values", produces a discontinue scatter diagram (not shown in this note).
-A base point on "the curve" is defined, rather randomly, but once chosen, it is fixed.
Usually, this base point (or reference point) is denoted by "G", but other letters are found
in the literature too.
Ofcourse, since we have now a discrete set of x-values, we cannot actually speak of "a curve",
but "G" is indeed an element on the scatter diagram, quite similar as if we still would have
used a continues curve.
-Using the analogy of a continues curve, just like above, we are able to perform a calculation
like:
5 * G = G+G+G+G+G
or:
n * G = G+G+...+G (n times)
-Likewise, a Public key can be derived using such system, using the equation:
Kpublic = kprivate * G
Where kprivate is a 256 bit number.
Note that the equation above, is not much different from an equation as "n * G = G+G+...+G (n times)".
It's a one-way system. It is commonly believed that it is not practically possible
to calculate the Private Key, from such Public Key.
2.4 A few words on Bitcoin Theft.
Here I can be very brief. You may wonder how I can talk about the security around Bitcoins,
while once in a while, large bitcoin thefts are reported.
This can happen if a "financial" institution is hacked, and Private Keys are stolen,
from such institution.
Some folks do not manage their wallets and/or keys themselves. They store them at such "financial" institution.
So, if that institution is hacked, and keys are stolen, then this is indeed theft. However, you cannot blame
the Bitcoin system. The Bitcoin system was deviced with a peer-to-peer intention, without any "financial" institution
involved, which collects active keys. If people or organisations store their keys at such central place,
in principle, that place can be hacked. As such, it has nothing "to do" with the Bitcoin system.
This concludes Chapter 2. (I need to finetune, and add some parts, but that's for later).
3. The process of Mining, and Transactions.
The "Bitcoin system" might even be viewed as a "Financial Revolution". However, I'am not really sure
if it really might be formulated this way. But many folks thinks that it's true.
⇒ For example, just look at the distributed Blockchain at all those different computing nodes:
It's rather remarkable. Don't forget all processing those full nodes perform, like checking
new blocks, peer-to-peer messages etc..
⇒ As another example, what do you think of the fact that a Central Authority is absent?
But not everybody is pleased with such an idea.
However, the idea of "Decentrialized Autonomous Services", which will use Blockchain technology,
to provide all sorts or relatively mundane services (insurances, logistics, contracts with all sorts
of service providers etc..) has already begun implementations.
The degree of automation of such services will be very high.
⇒ Then, overall security seems pretty tight too, and it must be said that in fact the technology
is "open", and transparant.
⇒ Then ofcourse, the existing blocks in the Blockchain, form an immutable ledger,
which is remarkable too in the financial world. Should be remarkable for auditors too.
There is also another highly remarkable mechanism at work in the "Bitcoin system".
It was already architected in Satoshi's original article: it's called Mining.
3.1 Mining.
A main theme of the Blockchain with respect to mining is realized by a chain
of "cryptographic puzzles", which are tried to be solved by a network of "miners".
A miner who successfully solves such a cryptopuzzle, is allowed to record a set of transactions,
and to create a new Block in the Blockchain. The more CPU and other computing resources are applied
by such miner, the more chance this miner has, to solve such puzzle.
As a "reward", bitcoins are granted to that miner.
The first transaction in a Block, is a special type of transaction, namely the "coinbase transaction".
The output of this transaction is coupled to the address of the miner and contains the reward.
Note that these bitcoins are "new" bitcoins.
Anyway, we know that miners try to create a new Block with yet unconfirmed transactions.
Note that in this system, a core statement could be:
Mining = transaction processing =
committing a new block with confirmed transactions to the Blockchain
Ofcourse, the procedure raises questions, such as "what exactly constitutes such puzzle"?
"Who can be miners"?, "What are their procedures"?
Secondly, does the procedure work, at all times?
A central idea of the Mining system is, that the majory of miners are "honest".
That is: The miners will do their work, driven to earn bitcoins. And most CPU power is distributed
among (assumingly) those honest miners.
Even if a couple of roque miners team up, and try to enforce certain wicked plans,
then they will always be outpaced by the majory of honest miners which control the majority of CPU.
Often this is called Proof of Work.
The next phrase is not speculation: suppose a smaller group of roque miners somehow
manage to aquire the majority of CPU power, then, will that group be able to control the system?
Theoretically yes, but in real World conditions, it is highly unlikely that this can happen.
At least we can say that an individual miner will never aquire sufficient resources to outpace the rest.
Still, It's an interesting question. Even if you would say it is not, we already now have touched upon
a basic idea behind the mining concept.
In fact, the "principle of majory" is fundamental in the mining business.
It's important to realize that the principle of mining, is paramount, at least for the Bitcoin Blockchain.
New transactions are collected in a new Block, and that Block will be collectively "approved"
to be valid by all nodes which are needed to reach consensus.
3.1.1 The Remarkable FeedBack systems in the Blockchain.
Increasing Difficulty:
The Bitcoin system, (sort of) aims to have a new block, every 10 minutes.
Ofcourse, this is not an exact number at all times. It's a sort of average.
Miners are able, after (statistically) an enormous amount of attempts, (or equivalently,
after applying enormous amount of CPU power), to guess the right hash.
This enables a lucky miner, to create a new Block with collected new transactions.
However, since CPU power have strongly increased since 2009 (the Start of the Blockchain),
and the organization of applying CPU power (in datacenters etc..) has also been optimized,
there is a risk that the condition of statistically 1 Block / 10 minutes, breaks down.
Therefore, there exists a "Difficulty target" in a block header, which determines how
many hash trials (guesses), on average, are needed to find the correct hash (or the solution
to the "cryptopuzzle").
The "Block creation duration" is aimed to be 10 minutes. The algolrithm is such, that after 2016 blocks,
the Difficulty Target is re-adjusted.
In figure 1, you can see that indeed a field of 4 bytes in the Block Header, is reserved for the Difficulty Target.
As such, the Blockchain uses a "FeedBack system" to control the amount of new blocks per time-unit.
Mining Rewards periodically get's halved:
This is a control mechanism for the amount of "new" bitcoins which the miners receive for their spend
CPU power.
As time progressed, CPU power rose too, and although the "Difficulty target" is a control mechanism
to limit the rate of new blocks to be about 1 Block / 10 minutes, another "mechanism" control the amount
of rewarded bitcoins to miners.
The algolrithm is, that the reward will halve every 210000 blocks.
So, once it was 50 bitcoins, then later it was halved to 25 bitcoins, and currently it amounts to 12.5 bitcoins.
3.1.2 The crypto puzzle to be solved by the Miners.
There is no "one Global" memory pool (mempool) of all unconfirmed transactions.
However, every node has such memory pool, and broadcasts, new transactions to peers.
Ofcourse, a particular node will also receive transactions.
This gives rise to a sort of appearance of a Global memory pool, however, every node
has it's own mempool.
When a new block is verified and accepted, all transactions which are in that block, will be
removed from the mempool (or mempools actually).
A typical size of that pool is around 3MB, which is indeed not very large (june, 2018),
and thus is about the size of 3 Blocks.
Note: throughout bitcoin articles, terms like "uncomitted", "uncomfirmed",
"incomplete", and "unsettled" are often observerd, for transaction which are not yet
permanently registered yet, in the Blockchain. It seems that the mempool contains transactions
which are most often labeled to be "uncomfirmed".
In the process of creating a new Block, Miners obtain a number of unconfirmed transactions
from a near mempool.
When the miners try to calculate a valid block, the following events are important.
The header of a new Block is in principle easy to construct, from the former block.
However, "the Bitcoin cryptocurrency network", or the miners, are confronted with
hashing-based "Proof-Of-Work" challenge. All active miners are confronted with that challenge.
Namely, the miner tries to discover, purely by trials (usually a very large number of trials),
a "nonce" number, that, when it is included in the new block, should come up with a hash
with at least a certain number of leading zero bits. The hash found this way,
is the solution of the cryptographic puzzle, and it's also often called "Proof-Of-Work".
Here is an example of such "correctly" (guessed) hash, found by some miner:
000000000000000000084b39789b2a8ae6dcaf4062906784442fe65de0f4de28 (june 2018).
The minimum number of leading zero's, relates to the "Difficulty Target" as was discussed above.
As time progressed, as of 2009, the number of leading zero's, increased on a regular basis.
Thus the difficulty increased too, to balance the enormous increase of CPU power (hashing power)
over the past years.
Next, we will try a somewhat deeper exploration of Bitcoin Addresses.
3.2 More on Addresses.
We already have seen this, but for easy reference, it's listed again.
In the Bitcoin system:
- A private key is 32 bytes long (or 256 bits).
- A public key is 64 bytes long, or 65 bytes (depending on coordinate perspective) See also below.
- A public Bitcoin address is derived, using multiple steps, from the Public key.
There exists even a few various formats of Bitcoin addresses.
Basically, a one way direction is formed by:
Private Key → Public Key → Bitcoin address.
But this is not the only way to obtain a Bitcoin address (see below).
Here is an example of a Public Key:
02b1633cafcc01ebfb6d78e39f687a1f0895c62fc95f51ead10a02ee0be551b4ec
A private key is a personal secret number which allows you to spend bitcoins.
You may have multiple Private Key's and multiple Wallets.
All your transactions are signed with hashes of your Public Key.
From section 2.3, we know that actually a Public Key is a point on an elliptic curve,
if indeed "elliptic key cryptography" was used to generate the Key.
In this system, the Private Key is used, to generate the Public key, using elliptic key cryptography.
However, multiple ways exist to generate a Public Key, and it does not need to use
elliptic key cryptography, perse. For example, RSA (like RSA-256), is much used too.
Public key length, or, coordinates:
From section 2.3, we know that a Public key, calculated as "Kpublic = kprivate * G",
is actually a coordinate, expressed as (x,y). For details: see section 2.3.
This gives a difficulty in sayin that a Public key in elliptic key cryptography, is 32 bytes long,
since it is not.
For a Private key, we do not have such difficulty, since that is just a scalar (just a number).
In the secp256k1 specification, we then have an "x" coordinate of 32 bytes, and a "y" coordinate of 32 bytes,
as the components of a Public Key (in elliptic key cryptography). Note: In other methods likes RSA, this is not an issue.
So, how do we deal with something that actually "looks" like a vector, or point in R2?
A few solutions:
-If you consider the x and y, to be simply hexdecimal strings of characters [0..9,A..F], or represent them
in hexadecimal format, you could concatenate them (glue together) to arrive at a 64 bytes long string.
-You could also wonder, why not simply only the x or y coordinate is used?
It's a good question, and in modern client software, such procedure is nearly used indeed, apart
from some difficulties in the "sign" of such coordinate component.
So, what they have come up with, are multiple methods, where an additional leading "byte" specifies
which method is used. Here are a few examples:
0x04 (32 byte X coordinate + 32 byte Y coordinate), resulting in a 64 byte key, or 65 byte construct.
0x02 (32 byte X coordinate), resulting in a 32 byte Key, plus a parity designating byte.
The latter is also called, a "compressed Public Key". Note that even more "constructs" exists.
Bitcoin Addresses:
A Bitcoin address represents a destination for a Bitcoin payment.
Above we have seen that an adress is formed by Private Key → Public Key → Bitcoin address.
The derivation of the adress involves steps using SHA-256, RIPEMD-160 and Base58Check.
At least, that should make everything uniform. But in reality, it is not, due to certain reasons.
To generate an address using other methods, is possible too.
In general, we have:
- P2PKH, or "Pay to Public Key Hash", a string which starts with "1", and is derived
from the Public Key, as we already have seen above.
- P2SH, or "Pay to Script Hash", a string which starts with "3", and is based
on the Bitcoin scripting language.
- Bech32 type, a string starting with "bc1". It is especially meant for
the segwit implementation, and as such it is a SegWit address format.
3.3 More on Transactions.
4. Just a few words on Smart Contracts.
4.1 Introduction.
A Blockchain implementation, might be used as a basis for Smart Contracts as well.
Then, instead of focussing on payments and registering such transactions, the code involved
is likely to use more "semantics" to specify the conditions and actions to achieve the goal of
the specific "Smart Contract".
Many folks say that the code involved, must be (or should be) "Turing-complete",
that is (more or less), as set of instructions that can be seen as sufficiently complete
to implement "a machine" with exact predictible outcomes.
Associated with the conditions and actions, might be a digital document which is stored
and replicated with that specific Blockchain.
The many copies of the "contract", gives the same benefits as is true with the Bitcoin Blockchain.
However, since the code usually has more semantics (more complex), an unexpected bug
might present rather unfriendly situations. Ofcourse, the parties involved in developments
in this domain, are aware of this.
Is a Blockchain absolutely needed for the implementation of a Smart Contract?
For now: Yes. At the moment, it's a good means for implementing Smart Contracts. And contrary, "Central solutions"
are just the stuff that is tried to be avoided using e.g. Bitcoins and, indeed, also with Smart Contracts.
A similar system as is used in the Bitcoin blockchain, does provide support for implementing smart contracts,
like a replicated blockchain, miners collecting transactions, untrusted users, immutable ledger,
no Central Authority etc.. Thus indeed, the answer is "yes" (for now).
However, the code that's used for smart contracts, needs to meet certain requirements.
It does not need to be extremely intelligent parsers or compilers, but rather
mundane semantics are required, like decision logic (like if..then..else), and loops, and branching etc..
In general, a smart contract is synonym to executable code that runs on a blockchain, together
with supporting facilities (like e.g. mining) to execute and enforce the terms of any suited agreement
between (untrusted) parties.
One very promising platform, using a Blockchain implementation, is the "Ethereum" platform,
which many folks call "The Blockchain App" platform.
However, smart contracts better have a slower, very precise, implementation.
If you look at Bitcoin, it has proven itself over many years now.
But if a hausse of smart contracts are poored over us, then consider the fact that
bugs, miscoding and the like, in smart contracts have direct economic consequences,
and are irreversible.
4.2 A simple example of a smart contract.
Please do not have "high" expectations of this section, since it is extremely simple too.
However, a supermodern stealth fighter jet, and a old biplane from 1925, both share the
most important property: they both fly using the same basic principle.
Ethereum is more of a "programmable" blockchain, if you would compare it to the Bitcoin blockchain.
The Ethereum nodes in the network, run the Ethereum Virtual Machine (EVM).
The EVM runs "bytecode", and the whole principle has quite a few similarities to the
well-know Java Virtual Machine (jvm for java apps), or the CLR of the .NET environment.
However, this time it's completely de-centralized.
And, just like e.g. the JVM is the runtime for Java apps, similarly, the EVM is the runtime for smart contracts.
A contract itself, thus "live" isolated, and for network and other services, it simply
uses (or requests) the methods of the EVM.
The first programming environment on Ethereum, is called "Solidity". It has many OO features,
and offer most of what traditional developers already know, like functions, private/public
data and functions etc.. etc..
However, developing on Ethereum is not limited to Solidity. The list of dev environments, is growing.
If you compile your Solidity source, it will be "bytecode" than can run in an EVM.
A smart contract is stored as bytecode in the Blockchain with a transaction, and while running,
arrays, key-value pairs etc.., is stored in Merkle "tries" on the node.
Costs are in effect in Ethereum: the unit of fee is called "Gas", and it is the intrinsic pricing
mechanism for running a transaction or contract in Ethereum.
There are really nice intro's on the Internet, which gives good orientations on developing
and deploying a smart contract. The article below, is such an article.
The code the author uses, is very simple, since it's only a "counter", but he
succeeds in showing a methodology of creating smart contracts in Ethereum.
Besides showing how to create and deploy one, it also gives good idea on the Ethereum environment itself.
If you like to try that article, you can find it here (medium.com).
Epilogue (sort of):
Just a few lines:
- I like the technologies around cryptocoins, but I am sure that e.g. the socio-economic impact
might be huge, and maybe, is not exactly what everybody wants..
I think that there still is room, for more comprehensive social-economic studies.
- The energy consumption of "mining", might be somewhat troublesome as well.
Over the last few years, it increased sharply. So how will that develop in the next years?
It seems that thorough scientific research, is still missing.
I really would like to see some well-backed figures and forecasts.
(1): Readers comment:
Isn‘t it better to compare this with the use of energy for mining gold...or the use
for the existing "old" system with ATM‘s, banks, controlling, printing, counting and
hold money in the present form together with creditcard Systems alive?
Have you any idea how much more you can multiply the use of electricity for bitcoin to
come to this of the old system?
Answer: Indeed this comment, might put it in a certain perspective.
However, the problem is that scientific data, or well-funded estimates seem to be missing.
So, I don't have well-backed ideas, but there are indications in some articles
which are a bit worrying. That's why I wished that researchers would came up with
numbers on how it is "now", and would show us some realistic forecasts.
And how to compare that energy footprint, to the energy footprint of the Legacy systems,
which may even diminish somewhat in numbers and volume... At this time: No idea at all.
Any comments?
Then contact me at albertvandersel@zonnet.nl
Thanks !



