Maybe you need to learn basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

1. Positions in a Coordinate Sytem for the "plane".

In a flat "plane", we often should be able to pinpoint, or exactly describe, positions.

Long time ago, mathematicians deviced a rather nifty method to accomplish that purpose.
They designed a "grid", with a well-defined point of reference. This special point, is often called
"the Origin". Next, two perpendicular "axes" are drawn, which intersect exactly at the Origin.
The horizontal axis, is called the "x-axis". The vertical axis, is called the "y-axis".

So how do we pinpoint "points" in that Coordinate system?
Take a look at figure 1.


Figure 1. Coordinate system (in the plane).



From the Origin (O), if you take 3 steps to the right, you are at x=3.
Or more precise, if you take 3 steps to the right, you are at x=3 and y=0, since you never moved "up" or "down"
along the "y direction" at all.

In the next example, we will move in both the x- and y directions.
From the Origin (O), if you take 3 steps to the right, you are again at x=3.
If you now, from that position (x=3), take two steps up in along the y-direction, then you
arrive at x=3 and y=2. The way how often mathematicians write that down is: we are at point (3,2).
Do you see the point (3,2) in figure 1 above?

We do not only have positive numbers like 1, 3, 12, 1000 etc.., but negative numbers as well.
Those are numbers like, for example, -1, -3, -12, -1000 etc..
If you are not "comfortable" with negative numbers, then in this link (section 3),
I try to explain it a bit. However, you do not need to go to that link. You can also see it this way:

In the Coordinate system, if we take steps to the right on the x-axis, we go to points like x=1, x=7, etc..
However, if taking steps to the left, thus in the opposite direction, we have ("sort of") no other choice
than using different numbers. You know, the positive ones are already taken.
But it really makes sense to denote "moving to the left" as saying that we go to x=- 1, x=- 7 etc...

It makes it completely "symmetrical". For example, from the Origin, if you take 5 steps to the right,
you go to x=5. But, if you, from the Origin, take 5 steps to the left, you end up in x= - 5.
In such a way, 5 steps to the right, or 5 steps to the left (from "O"), have the same absolute distance.
In fact, only this way we have a truly usable Coordinate system.

As a last example, note the point (-3, -3) in figure 1. It means: x= - 3 and y = - 3.
If you want to "pinpoint" the position, you may say: it's the point where x= - 3 and y = - 3.
But it's much easier to pinpoint it by using the notation (-3,-3).
In words: (-3,-3) means: from the Origin, I take 3 steps to the left along the x-axis, and
I take 3 steps down along the y-axis.

2. Linear equations: they are just "lines" in a Coordinate system.

Next we are going to study "linear equations", which are equations of the form "𝒴=a𝒳 +b".

I will explain the equation in a minute. But first a few words on how we write it down.

About the "format" of such equation:

If you look at such equation "y=ax+b", then you must know that here "x" plays the role as the variable
along the x-axis, and not the multiplication symbol. That symbol is usually simply left out.


Now about the meaning of such equation.

If you see such a formula for the very first time, I can understand that you think "What is that!???".

We already have seen the Coordinate system with the x- and y axes. You can define, or pinpoint, "points" in the plane,
by specifying the exact "x" and "y" for such a point, like for example the point (2,4).

Let's take a look at a specific example, like "y=2x".
And.. let's see what happens with the value of "y" if we fill in a couple of "x values". Here we go:

Table 1: calculate "y" for a number of x values.

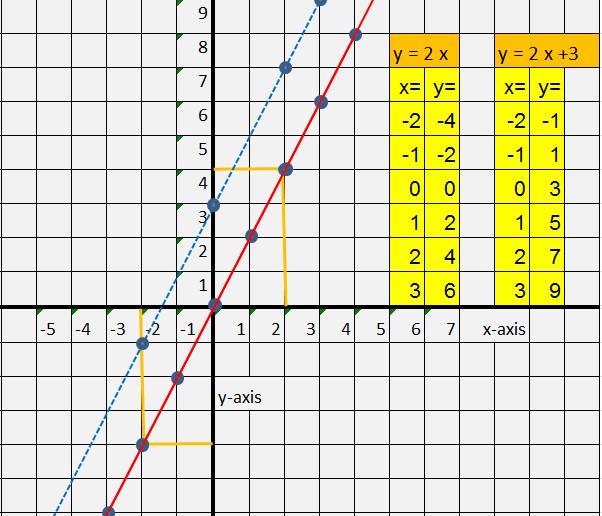
value of x:	value of y: (which is 2x)
x= -2, then	y= -4 (because 2 x -2 = -4)
x= -1, then	y= -2 (because 2 x -1 = -2)
x= 0, then	y= 0 (because 2 x 0 = 0)
x= 1, then	y= 2 (because 2 x 1 = 2)
x= 2, then	y= 4 (because 2 x 2 = 4

Figure 2. The functions y=2x and y=2x + 3



In figure 2, we simply have plotted the points from Table 1, into the Coordinate system.
If we connect those dots, we simply get a line ! See the red line in figure 2.

We may conclude that if we put the equation "y=2x" into the Coordinate system (by calculating y values,
for a certain number of x values), we then find a line. A line is also often called "a linear equation".
So, an equation like "y = ax", where a is just some constant number, can be represented by a line.

You could perform a similar action for other equations like for example "y=5x" etc..

By the way: note that for drawing a line, you actually need only two points.
You may ofcourse calculate for a larger number of "x-values", what then the resulting "y-values"
will be, just like we did in Table 1. But actually, doing so for 2 points only, is enough.

So, we analyzed the equation "y=2x" and saw how we could plot points in the Coordinate system.
That example stands model for any sort of such equation "y=ax", where "a" is some number.

However, a general linear equation is this:

y=ax +b

So, what's the story with "b"?
Well, in figure 2 I have placed the example line "y= 2x +3".
Note that for all x on the x-axis,, that line is exactly "3" above "y= 2x"
So, it's always 3 above "y= 2x" with respect to the y values.

Does that make sense? Take a look again at both examples:

y= 2x
y =2x +3

Yes, the only difference is the '+3', which means that for all x on the x-axis, y is always '+3' larger
compared to the equation "y=2x".
In figure 2, notice the blue line. It's the line "y=2x +3".

Question: could you create a similar table like Table 1, but this time for "y=2x +3"?
By the way, the answer can be found in figure 2 as well. Note the column on the right side.

=> The Power of a linear equation:

Actually, the real power of having an equation, like for example "y=7x -5",
is that you immediately can calculate "y", for any x

For example, you do not need to draw a line first in a Coordinate system. Say x=30, then y=7x30 + 5 = 215.
And that holds for any "x". Just do the calculation, and you know the value of the corresponding "y".

=> A special case:

In general, we have the equation "y = ax +b", where "a" and "b" are some specific numbers.
For each different "a" and "b", we have a different line in the Coordinate system.

However, what happens if "ax=0"? Then we simply have "y=b".
This means that, for every x along the x-axis, y remains the same, namely "y=b".

So we could have the line "y=5", or "y=-7" etc.. These lines are parallel to the x-axis, since y remains constant.

Here are some examples:

Figure 3. Some examples of the equation "y=b" (thus y is constant).

=> Another example of y=ax +b:

This time, we will take a look at the line "y = -3x + 2".
Here, the number "a" is a negative number. Nothing changes fundamentally, however, if you are really
new in this business, you just need an example of such a case.

Let's draw the line, with the help of a table, similar to Table 1.
But..., you need to know a certain fact beforehand. Maybe you already know this, or not, in which case in cannot hurt.

Here is what I mean:

a positive number X a positive number = a positive number. For example 5 x 5 = 25
a positive number X a negative number = a negative number. For example 5 x -5 = -25 (note the "-" signs).
a negative number X a negative number = a positive number. For example -5 x -5 = 25.

So, for example 5 x 5 maybe seen as "Do 5 times, 5 steps to the right from the Origin",
which will put you at x=25.

For example, 5 x -5 maybe seen as "Do 5 times, 5 steps to the left from the Origin,
which will put you at x= -25.

For example, -5 x -5 maybe seen as -(5 x -5) = - (-25) = 25
which will put you at x= 25.

Indeed, a "negative number" times a "negative number" is positive.


Ok, it's time to draw the line:

Table 2: calculate "y" (y = -3x + 2) for a number of x values.

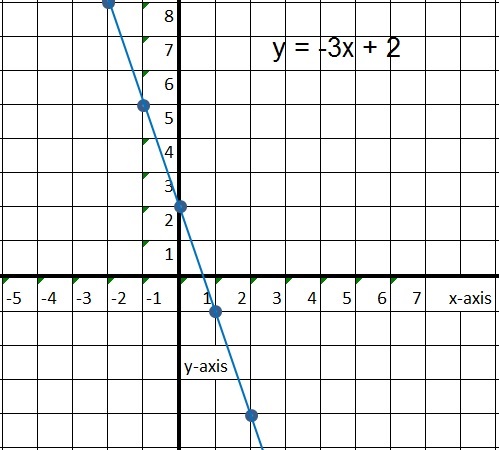
value of x:	value of y: (which is -3x + 2)
x= -2, then	y= 8 (because -3 x -2 + 2 = 6 + 2 = 8)
x= -1, then	y= 5 (because -3 x -1 + 2 = 3 + 2 =5)
x= 0, then	y= 2 (because -3 x 0 + 2 = 0 + 2 = 2)
x= 1, then	y= -1 (because -3 x 1 + 2 = -3 + 2 = -1)
x= 2, then	y= -4 (because -3 x 2 + 2 = -6 + 2 = -4

Since we have two or more points of this line, we can draw it now:

Figure 4. The line y = -3x + 2.



Ok, let's go to the next and last section.

3. Solving linear equations.

Well, a linear equation like "y=ax +b", holds for all x's and y's, or in other words, it is a certain relation
between x and y in the entire Coordinate system.

Solving an equation can mean that you can calculate a specific "y" value for a specific "x".

For example:

What is the value of "y" if x=3 for the equation y=5x +2 ?

Answer: y= 5 x 3 + 2 = 15 + 2 = 17.

However, what is usually meant by solving, is finding "special points".

Any line (except the horizontal and vertical lines), will "intersect" with the x-axis and y-axis.
Finding those (x,y) points, can be of great use:

1. Intersection with the y-axis:

At such a specific point, thus where the line crosses the y-axis, then we know for sure that "x=0".
Take a look at the figures above.
From those examples, you can really see that at intersection with the y-axis, then x=0.

Thus for that specific point:

y= ax +b and with x=0, we have y= a x 0 + b = b

For example: the line y=2x + 3 crosses the y-axis at: x=0 and y=3, or the point (0,3).

2. Intersection with the x-axis:

If a line crosses the x-axis, then at that specific point, y=0.
Take a look at the figures above. At the x-axis, the height of y is zero, so y=0 at that point.
Thus:

y= ax +b and if y=0, then ax +b =0, thus x=- b/a

Note:

If we have: ax + b = 0
Then we may add "-b" to the left side- and right side of the "=" sign. Thus:

ax + b = 0 =>
ax + b -b = -b =>
ax = -b =>
x= -b/a

So, for example, suppose we have the line y=2x +4. Where does it intersect the x-axis? At that point, we know for sure that y=0. So:

2x + 4 = 0 =>
2x + 4 -4 = -4 =>
2x = -4 =>
x= -4/2 = -2

So, this line intersects the x-axis at x=-2, or at the point (-2,0).

3. Intersection of 2 lines at some point:

Two lines which are not parallel, will intersect at a certain point. Ofcourse, since the lines are straight,
there can only be one such point.
See figure 5 for an illustration.

Figure 5. Intersecting lines



One thing is for sure: where they intersect, at that one point, the lines share the same "x" and "y".

So, suppose we have:

y= -3x - 3
y= -x - 1

Since at that point y=y, we have:

-3x + 3 = -x - 1

Since an equation stays the same if on both sides of the "=", the same is added.
Let's add "x" to both sides:

-3x + 3 + x = -x -1 + x

thus:

-2x + 3 = -1

Add -3 to both sides:

thus:

-2x = -4

thus:

x = -4/-2

x = 2

So, at least the x-coordinate is known. It's x=2. Now you can use either of both equations to calculate
the y-coordinate. Let's use "y= -x - 1". Thus y = -2 - 1 = -3.
Thus we have found the point (2,-3), where both lines intersect.

4. Some formal terms.

In this short section, we will do no calculations at all!
It's just good, to introduce a few formal terms here.

When you look at a general linear equation:

y = ax +b

then mathematicians also say that y is a "function" of x. This is also written as f(x).
In other words, each "y" depends on a certain "x", and y is defined by ax +b.
It's absolutely no more than a "formal" way of saying things.
Thus:

y = f(x) = ax + b

If y=ax+b is a function of x, then some also say that the equation can be interpreted as:
x is mapped to y, or x -> y (which is a short form of saying "x is mapped to y").

That's it. Hope you liked it.
The next note as about quadratic functions and higher order polynomials.