In the series: Note 18.
Subject: Permutations and Combinations
Date : 7 November, 2019Version: 0.5
By: Albert van der Sel
Doc. Number: Note 18.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
This note: Note 18: Simple introduction in Permutations and Combinations.
Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 17.
This will be a relatively short note. We will see what n! means, and we will study a few scenario's
from "counting theory". The latter is involved in questions like how many sets of "k" elements
can we create from "n" elements?. Here, various boundary conditions might be involved too, like
no repetitions of those k elements allowed, or contrary, repetitions of those k elements are allowed.
As examples of such questions:
Suppose you have three elements "A", "B" and "C". Thus we have the set {A,B,C}
Question 1: How many ordenings can you create, without repetitions of such element?
Like: ABC, CBA etc..
or:
Question 2: like question 1, but this time repetitions are allowed.
Like: AAB, CCA, BAC, BBB etc...
or:
Question 3: Suppose we have the elements A and B. How many 9 element ordenings can we create
where repetitions are allowed, like for example AAABAABBA, BBBABBAAA etc..?
So, how to handle such things? This..., we will see!
But first, we need to know what "n!" is, and we need a few terms to be explained.
1. What does n! mean?:
The notation n! is often said to be the "faculty" of n.Here, "n" must be an integer, like 0, 1, 2, 3, etc...
It's really simple. For example:
3! means: 3x2x1=6.
5! means: 5x4x3x2x1=120.
Now, n! is thus defined to be:
n! = n x (n-1) x (n-2) x .. x 2 x 1 (equation 1)
As another example, if we must calculate 10!, then it's equal to 10x9x8x7x6x5x4x3x2x1.Furthermore:
0! is defined to be "1", so 0!=1.
By the way, do you agree that:
n! = n x (n - 1)!
Yes, sure that's true. Since:
n! = n x (n-1) x (n-2) x .. x 2 x 1
n x (n - 1)! = n x (n-1) x (n-2) x .. x 2 x 1
So indeed: for example 5! = 5 x 4!
Some math is possible too, for example:
4! x 3! = (4x3x2x1) x (3x2x1) = 24 x 6 = 144.
or, something like:
|
3! ----- (3-2)! |
= |
3 x 2 x 1 ---------- 1 |
= 6 |
A special form is the "n choose k" format (n over k format), which you can see below.
|
n! ------- k! (n-k)! |
(equation 2) |
As an example of equation 2, were "n"=6 and "k"=2:
|
6! -------- 2! (6-2)! |
= |
6x5x4x3x2x1 -------------- (2x1) x (4x3x2x1)! |
= |
6x5 --- 2 |
= 15 |
Note: equation 2 is also know as the "Binomial coefficent".
We will see this in a later section, where equation 2 is the solution for the question of "how many
combinations can we create, of k elements out of n elements".
Equation 2, has a shorthand notation (which looks like a vector, but is not):
|
┌ n ┐ └ k ┘ |
= |
n! ------- k! (n-k)! |
(equation 3) |
2. The difference between Permutations and Combinations:
Note: some articles speak of "elements" and others of "objects", or similar terms,but it is all to mean the same thing.
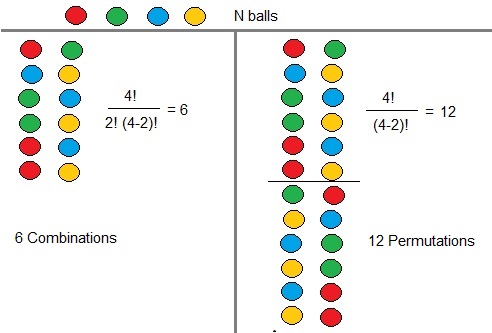
In the figure below, you see 4 coloured balls. You could call them objects, or elements,
or you may use some other fancy term.
Take a look at the figure below. Here we have 4 coloured balls.
One question might be: how many "arrangements" of 2 balls can we create from those 4 balls?
Note: it does not have to be "2", for example, we might also have asked how many
3 ball arrangements, can we create from those 4 balls.
Or more generally: how many arrangements of "k" objects can we create from "n" objects?
->With Permutations, the order of the elements does matter.
The order does matter, so an ordening like ABC is different from BAC, while still
both ordernings use the same elements (characters).
If you look at the figure above, on the right side you see that we have 12 permutations
of two coloured balls, out of 4 coloured balls.
Here, order "matters", for example a "RED-GREEN" arrangement, is different
from a "GREEN-RED" arrangement.
->With Combinations, the order of the elements does not matter.
So, an ordening like ABC is not different compared to BAC: the ordening does not matter.
If you look at the figure above, on the left side you see that we have 6 combinations
of two coloured balls, out of 4 coloured balls.
Here, order "does not matter", for example a "RED-GREEN" arrangement, is equivalent
to a "GREEN-RED" arrangement.
From Wikipedia: "In mathematics, a combination is a selection of items from a collection,
such that (unlike permutations) the order of selection does not matter."
Indeed, it's almost that easy. The illustration with those coloured balls hopefully helps
to understand the difference between "permutations" and "combinations".
Usually, a Permutation/Combination is considered to be an ordening of k elements out of n elements,
without repetitions. However, in the literature, you may find the phrases "permutation with
or without repetitions". Again, for both it usually means taking k out of n, without repetitions.
The only difference between a Permutation and Combination, is about the "order" of elements.
Let's illustrate this with a few examples. Those are only here to demonstrate
the difference between Permutations and Combinations. Actually, we already have seen it
in the example above with the coloured balls.
Suppose we have the set {A,B,C}.
Example 1: How many Permutations (without repetitions), can we create?
A key question is: how many different unique arrangements, without repetitions, can we create out of that set?
Folks also rephrase that as: How many Permutations without Repetition can we create out of that set?
In such a permutation, the ordening of the elements is most important. That is: it matters.
Formally, a "Permutation" is understood to take "k" elements from "n" elements, without repetitions.
Note that:
-An ordering as for example "AAB" is not allowed, since we require "without repetitions".
-The arrangement as for example ABC is different from CBA, since they are ordered differently.
You can use plain and simple logic here. For the first element, we can choose from 3 elements. Then, for the second element,
we can choose from 2 elements (thus one less), and for the third element, we can only choose one (thus 2 less).
No matter with which element you start with, the above reasoning will always hold.
Let's work out our simple example. We can only create the following unique arrangements:
A B C
A C B
B A C
B C A
C A B
C B A
-Remember, that in this example, we need to find the "Permutations without Repetition".
That means that for example AAB is not allowed, since then we repeat the "A".
-Remember that here ABC and CBA are regarded as "different", since they are ordered differently.
So we have 6 unique arrangements (Permutations without Repetition).
You can try to find more, but it will not work.
Suppose again, we have the set {A,B,C}.
Example 2: How many Combinations without repetitions, can we create?
In this case, it's only one! Since the order does not matter, ABC is equal to all other arrangements.
In later examples, like taking "k" elements out of "n" elements, we see different combinations.
It's indeed true that the term "combinations" in counting problems, is a bit counter-intiutive.
Next, we will study several cases of Permutations and Combinations, of "n" elements, or
"k" elements out of "n" elements.
Important: Naming conventions: Variations instead of Permutations (k out of n elements)
Some articles and textbooks, take "permutations" to be ordenings of "n" elements only.
So, if you take "k" elements out of "n" elements, those texts speak of "variations",
or "k permutations of n", instead of (pure) permutations.
It's probably not "world shocking" news, but you must be aware of it.
3. Ordenings of "k" elements out of "n" Different elements With possible repetitions:
You may use the term "permutation" here, but that's usually reserved for choosingk elements from n elements, without repetitions (or just permutations of "n" elements).
That's why I use the term "ordenings" in the title of this section.
But, many folks use the term "permutation" anyway.
You can use plain and simple logic here. For the first element, we can choose from "n" elements.
Then, for the second element, we can choose again from "n" elements. And you do that "k" times.
Remember, repetitions are allowed, so at each choice, we have "n" elements to choose from.
So without proof, we say:
Number of ordenings of "k" elements out of "n" different elements, with repetitions is:
n x n ...x n (k times) = nk; (equation 4)
Here, we have "n" elements to choose from, and we do that "k" times.Example:
Suppose we have the set {A, B, C}.
How many ordenings of "2" elements out of "3" Different elements With possible repetitions can we create?
You can manually work it out, and find:
AA
BB
CC
AB
BA
AC
CA
BC
CB
We find 9 ordenings (with repetitions). This is indeed 32
Another example:
Suppose you have 2 basic elements, like "A" and "B".
Suppose further you must create "sets" of 9 elements, like "AABAABBBA" etc.., where repetitions
of "A" and "B" are allowed.
Question: How many different sets can you build?
First, it's important to realize that we may use repetitions here, like "AABAABBBA", or "BBBBBBBBA" etc..
It's fully similar to "bitstrings". If you have "0" and "1", how many different sets can you build with a length of 3?
The full set is:
000
001
010
011
100
101
110
111
So, here the answer is 8. Note that this is equal to 23.
It turns out, that if you have "n" different elements, and you must create sets with a length of "k",
where repetitions are allowed, the answer is:
number of different sets (with repetitions) = nk
If we return to our example of ordenings of 9 elements, with the set of elements "A" and "B", then:-n=2
-length=9
-repetions are allowed
So, the answer is 29=512.
4. Permutations of "k" elements out of "n" Different elements Without repetitions:
Suppose we have the set {A,B,C} again.How many different Permutations, of 2 elements out of 3, can we create out of that set?
Remember, here we no repetitions of elements.
Here I simply say that the answer in general (arbitrary "n" and "k") is:
|
n! ----- (n-k)! |
(equation 5) |
So, here "k"=2 and "n" =3. Using equation 5, this will yield:
|
3! ----- (3-2)! |
= |
3 x 2 x 1 ---------- 1 |
= 6 |
If we just write it out, we get:
AB
BA
AC
CA
BC
CB
So indeed, 6 is the answer.
You see that the result of equation 5, and the manual method, leads to the same result.
This is not a proof, but as usual, I like to make things a bit plausible.
Another example:
Suppose "n"=8, and "k"=3, and we want the number of possible
Permutations without repetitions:
|
8! ----- (8-3)! |
= |
8! -- 5! |
= |
8x7x6x5x4x3x2x1 --------------- 5x4x3x2x1 |
= | 8x7x6 | = 336 |
Let's now see an example with Combinations.
With Combinations, the order does not matter, so BA is the same as AB and counted as one.
Indeed, in general, in a similar problem, the number of Combinations is lower
than the number of Permutations.
5. Combinations of "k" elements, from a set of "n" elements:
Remember, when finding "combinations" the order of elements does not matter.Using "induction", it's not too hard to prove the theorem below. However, considering the "weight"
of my notes, making something "plausible" is often sufficient.
Suppose we have the set {A,B,C} again.
How much combinations of 2 elements can we create?
Manually, we find:
AB
AC
BC
In section 4, we had the same question, but there we wanted the number of Permutations
without repetition, and we ended up with "6".
If you look again at equation 5, then we need to remake the formula in order to get
a smaller result. Yes, if we divide with k! as an extra element in the denominator,
we get the right results.
Here I simply say that the answer in general (arbitrary "n" and "k") is:
|
n! ------ k!(n-k)! |
(equation 6) |
You can check our upper example with this formula:
|
3! ------ 2!(3-2)! |
= | 6 / 2 | = | 3 |
Seems to work out.
Note that this is exactly as what we already saw in section 2, the Binomial coefficent (equation 3):
|
┌ n ┐ └ k ┘ |
= |
n! ------- k! (n-k)! |
6. Sum- and/or Product rules with independent events:
Up to now, we considered one "event" like taking "k" elements from "n" elements,and then see in how many ways those k elements can be arranged.
As we know, it still can be important to know if "the order" matters, or not,
which determines whether we are dealing with a Permutation or Combination.
This section is a bit different.
How to handle things, if we are dealing with two or more independent "events"?
As it will turn out, it depends on how you can interpred the sitution
as being "AND" or if you would interpred it as being an "OR" situation.
Let's illustrate this with an example. Take a look at the figure below:
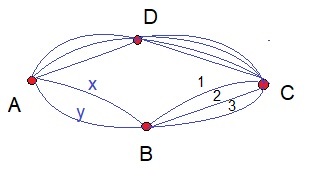
Suppose we have 4 cities, namely "A", "B", "C" and "D".
Similarly, going from "A" to "B", then you have two roads to choose from.
Going from "A" to "B", I labeled those two roads as "X" and "Y". Similarly, going from "B"
to "C" can be done choosing one of the three roads, labeled as "1", "2", and "3".
Case one: One initial event.
Suppose point "D" is not there, for this particular experiment. So here, we only consider the
the points "A", "B", and "C". Next, suppose you need to go from point "A" to point "C".
Now, there is no direct route from "A" to "C", meaning that you will always pass point "B".
What are the options?
-From A to B, we can choose from road "X" and road "Y".
-From B to C, we can choose from the roads "1", "2", and "3".
So, all possible full tracks (A->B->C) seem to be: X1, X2, X3, and Y1, Y2, Y3.
So, the total ammount of routes from "A" to "C", going through "B", seem to be "2x3=6".
Why is it "2x3" and not "2+3"? If you would evaluate the sitution, using common sense,
it might be evident to be "6", since you can simply count all possible options.
Indeed, all tracks (A->B->C) are: X1, X2, X3, Y1, Y2, Y3.
Is "plain logic" enough here? No, not really because you might like "proof"
for a generalized situation. But please note, while counting all options,
you do an "AND" operation all the time. It's X1+X2+X3+Y1+Y2+Y3.
That is "2x3=6". I agree, it's not mathematically "clean enough". But what's to be expected from Albert?
Case two: Two initial events.
This time, we will consider "D" too, to be a possible node in the path from "A" to "C".
Note that we can have: A->B->C OR A->D->C.
Route A->B->C: there are 6 possible options.
Route A->D->C: there are 12 possible options (check this).
So, what would be the Total amount of possible routes?
This time we need to take into account A->B->C or the routes belonging to A->D->C.
In this example, the number of routes from "A" -> "C" is: 12 + 6 = 18.
This makes sense.
- We already have seen that from "A" to "C", going through "B", is "2x3=6" routes.
- The other option is from "A" to "C", going through "D", is "3x4=12".
There is no other answer, then concluding that the total amount of routes is "6+12=18".
In general, when you see AND conditions, like counting routes, we Multiply.
Likewise, in general, when you start with OR, then you Add the outcomes of the subsets.
Optional Reading: some more explanation about AND or OR:
Suppose you throw a dice, once, or two times.
What is the probability you throw a six the first time, AND a six the second time?
P(6 AND 6) = 1/6 x 1/6 = 1/36 (note the Multiplication)
What is the probability you throw a six OR a four at your first throw?
P(6 OR 4) = 1/6 + 1/6 = 2/6 = 1/3 (note the Addition)
7. Summary, or a compact scheme on how to find a solution for one event:
There are many examples out there on the theory of "counting".As a general guidance, you may take a look at the following scheme on how to find
a solution for one event (like selecting k elements from n elements).
It's not fully watertight, but may help in many cases.
(1). What is the total set, or, out of how many of elements do you choose from: That's "n".
(2). How many elements do you choose or pick: That's "k".
(3). Is Repetion allowed, or, can you choose the same element again?
→ Yes. Answer likely to be nk
↓ No
→ Permutations: "k" elements out of "n". Order does matter. No repetitions.
|
n! ----- (n-k)! |
If we do not have "k" elements out of "n", but we simply want to find the number of
permutations of n elements, the answer is: n! (permutations of n elements).
→ Combinations: "k" elements out of "n". Order does not matter. No repetitions.
|
n! ------ k!(n-k)! |
→ Sum- and Product rule:
With two or more independent events:
-If you can relate it to AND, then multiply the outcomes.
-If you can relate it to OR, then add the outcomes.
8. Tree diagrams:
An interesting aid for studying problems in counting, are "tree" diagrams.By fully drawing the tree, with all options, you might find a solution
for what at first looked like a complicated problem.
It will turn out to be a graphical representation for stuff we already know,
like "nk" or "n !" arrangements.
Example 1:
Suppose you toss a coin 3 times.
Question: Which possible arrangements (outcomes) can you get?
From the theory from former sections:
-For the first toss, you can have 2 outcomes (head or tail).
-For the second toss, you can have 2 outcomes (head or tail).
-For the third toss, you can have 2 outcomes (head or tail).
All possible ordenings are: 2x2x2 = 8.
Or all written out: HHH HHT HTT HTH THH TTH THT TTT.
You can represent this using a Tree diagram:
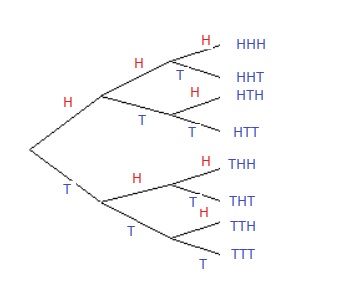
You first select for yourself, that branching "UP" stands for Head.
And, then you choose that branching "DOWN" stands for Tail.
Ofcourse, it makes no difference if you would have choosen the other way around.
If at each branching point, you then branch UP, and branch DOWN, you will get a Tree.
You must stop branching when you have reached 3 levels (because you tossed 3 times).
Note that you exactly get the same 8 ordenings: HHH HHT HTT HTH THH TTH THT TTT.
Also note that a avoided using the term "permutations". You may use it though.
But, permutations are more associated in general with solutions where we have:
nx(n-1)x(n-2)... etc.., so solutions which resembles n!, or using the exact formula
as is listed in section 7.
When we have solutions like "nxnxn.." etc..., it results to a set of outcome ordenings, which
many folks would not call "permutations".
Such a tree as above, is related to "power of", like e.g. 23, 24, nk.
Example 2:
In the former example, at each node, we always had two branches UP and DOWN.
In this example, it's a tiny bit more complicated. This time we do not have
repetitions, and once something is given away, the number of choiches decrease with "1".
Indeed, this more looks like having real permutations/combinations.
Suppose we have the following 3 employees:
"A", "B", "C".
Also, we have the set of 3 functions:
President, Secretary, Advisor.
Question: in how many ways can we arrange those functions over our employees?
Since "one function" is exactly mapped to "one employee", we can thus say:
-For the first employee, we have three choices.
-For the second employee, we have two choices.
-For the third employee, we have only one choice.
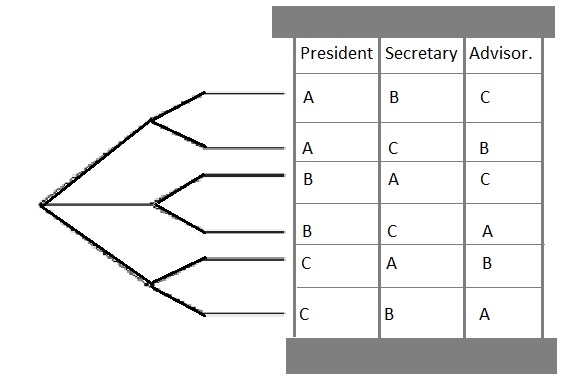
(rather ugly figure, I agree. But I hope it makes sense).
It's really a permutation. In this case the answer is 3! = 3 x 2 x 1.
To make it more clear: Now, suppose you had 10 employees, and 3 functions to give away.
Then we would have:
|
10! ----- (10-3)! |
= | 10x9x8 |
9. Some additional examples:
Example 1:
Suppose, in a waitingroom, we have 6 chairs. 4 people are entering this room,and they all take a seat.
Anyone of those 4 people, can choose any chair he/she wants.
Question:
How many possible permutations/combinations are possible?
Answer:
Possibly it's not immediately obvbious, but in this example, we have n=6 and k=4.
Why is that? You might say, that if someone chooses a particular chair, it is "just like"
that particular chair is selected in a "4 element, out of 6 element" arrangement.
Is it an example of a Permutation of a Combination?
This is not easy to answer. But, suppose Carla takes seat 2, and Andrew takes seat 3,
then we have a different arrangement compared to that Carla takes seat 3, and Andrew takes seat 2.
It strongly suggests that we have a Permutation. So:
| The number is: |
6! ----- (6-4)! |
= |
6x5x4x3x2x1 ---------- 2 |
= 360 |
Example 2:
Having seen some examples above, in relation to "combinations" and "permutations",will not immediately have you linked to the number of "routes" in a grid.
However, here too the theory can be applied.
Take a look at the figure below:
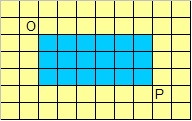
We need to go from point "O" to point "P", following the "grid".
Ofcourse, we must be involved only with the shortests routes, because if we are
allowed to step to the left, or step up, the number of possible routes is infinite.
So, we must stay in the blue region only.
Whatever route in the blue part you would take, it will be always 6 steps to the right,
and always 3 steps down. You can take any path you like, but the above is always true.
So, the total number of steps is "9" (always 6 steps to the right, and always 3 steps down).
Now, you will always take 6 steps right, and 3 steps down.
Would the problem be equivalent in finding all ordenings (possible paths) for 3 steps down,
out of 9 steps?
Would the problem be also equivalent in finding all ordenings (possible paths) for 6 steps right,
out of 9 steps?
Then, would you agree that the answer is:
|
9! ------- 3! (9-3)! |
But then, you might want to calculate the following too. Are they equivalent?
|
9! ------- 6! (9-6)! |
Indeed, if you calculate both, they end up to be equivalent.
Example 3:
Supppose we have 10 sporting teams, competing for the 1st, 2nd, and 3rd place.After the required number of matches, we finally found 3 teams for the 1st, 2nd, and 3rd place.
Question:
In how many ways, can we find different teams to end at 1st, 2nd, and 3rd place, out of
a total of 10 teams?
Answer:
Would it be considered a Permutation- or a Combination problem?
Well, since for example the podiumspots "UK-DE-US" would be different from "US-UK-DE", it would
be considered to be a problem to be solved using "permutations". Obviously, "order matters".
For the first place, we can choose from 10 teams.
Then, for the second place, we can choose from 9 teams.
Then, for the third place, we can choose from 8 teams.
The answer would be: 10x9x8 = 720 permutations.
Does this match our general formula for the number of permutations of "k" out of "n"?
Permutations: "3" elements out of "10" elements (order does matter).
|
10! ----- (10-3)! |
= |
10x9x8x7x6x5x4x3x2x1 -------------------- 7x6x5x4x3x2x1 |
= | 10x9x8 |
Yes, it matches the former calculation.
Example 4:
Question:Suppose you have a chessboard, with 8x8 (is 64) possible positions.
Suppose you have 8 castles. How many different arrangements can you create,
where each castle occupies it's own spot.
Answer:
You might say:
For the first castle, I can choose from 64 positions.
For the second castle, I can choose from 63 left positions.
For the third castle, I can choose from 62 left positions.
For the fourth castle, I can choose from 61 left positions.
For the fifth castle, I can choose from 60 left positions.
For the sixth castle, I can choose from 59 left positions.
For the seventh castle, I can choose from 58 left positions.
For the eighth castle, I can choose from 57 left positions.
That's all. So my answer would be: 64x63x62x61x60x59x58x57.
This would correspond to the number of permutations like:
|
64! ----- (64-8)! |
= |
64! --- 56! |
= | 64x63x62x61x60x59x58x57 |
Yes, it would be correct if each castle has it's own label (say a small unique flag),
which would make the order important.
However, in this case, order does not seem to matter. Each castle is indistinguishable from the others.
Thus, we must then calculate the number of combinations, which is:
|
64! --------- 8! (64-8)! |
That would be a smaller number, compared to the number of permutations.
It's a tiny bit philosophical, since on a microscopic level, each castle would
have it's own unique set of small scratches and irregularities, ofcourse.
This would make each castle unique, and then order would matter !
So then: does order matters after all?
Yes, it's an example where physical reality differs from an abstract example.
I think:
-for reality: calculate the number of permutations (order matters).
-for an abstract situation like an exam question: calculate the number of combinations (order does not matter).
How about that...?
Example 5:
See first, the upper part of the figure below. Here, A, B, and C are only connected by thethin (green) lines.
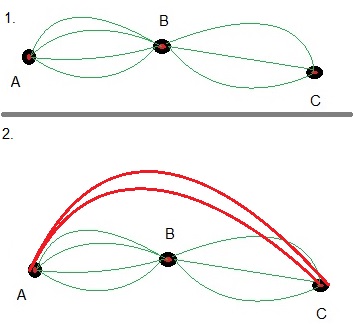
Question:
In how many "ways", or how many different routes, can I take to go from "A" to "C",
where I must pass "B"? (Here, consider the green lines only.)
Answer:
We have seen this before.
A->B: 4 possible routes.
B->C: 3 possible routes.
This is an "AND" situation, so we must "multiply" the outcomes of the subsets:
The number of paths going from A->C, passing through B, is "4x3=12".
Question:
Later, two new roads were constructed, which directly connects A with C. In the second part
of the figure above, these are the two fat red lines.
In how many "ways", or how many different routes, can I take to go from "A" to "C"
Answer:
-From A to C, going trough B: there are "4x3=12" possible paths, as we have seen above.
-From A to C, directly: there are "2" possible paths.
So what do you think? What's the total number of possible routes from A to C?
If it helps: Do you think you can associate the options to "AND" or "OR" problems?
Example 6: Pascal's triangle.
The following looks a bit like the possible number of routes in a grid.However, this time we have a triangle, where we start at the top.
We may ask: how many routes are possible, to go from the top, to any discrete point on the bottom line?
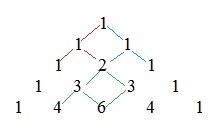
In the figure above, we only have a limited number of rows. Ofcourse, we can extend
the number of rows as far as we like.
We start at the top, and consider the number of "hops" or "steps", going from one point
to another below. Note that each time (at each point), you have two choices.
In the figure, we notate the sum of all possible number of hops, to reach that particular point.
Question: can you explain the number "6" at the bottom row?
Answer: directly above it, we already see the sums of the 2 point, which are the only ones
leading to "6". So, there are 6 possible routes to "6".
Question:
The number of routes leading to the lowest point on the left, is "1".
Note that this corresponds to:
|
┌ 4 ┐ └ 0 ┘ |
For the second point left, on the lowest row, we have:
|
┌ 4 ┐ └ 1 ┘ |
What do you think it will be for the third point (counted from the left side)?
This was just a simple note on "the theory of counting".
Much more can be learned. Let no-one ever stop you from learning more Math !!!